Container with most water problem

Today we are going to discuss another array-based question which is going to be a little bit tougher than the previous one.

The Problem

• Given n non-negative integers a1, a2, ..., an , where each represents a point at coordinate (i, ai).
• n vertical lines are drawn such that the two endpoints of the line i is at (i, ai) and (i, 0).
• Find two lines, which, together with the x-axis forms a container, such that the container contains the most water.

Notice that you may not slant the container.

Example 1:

1
2
3
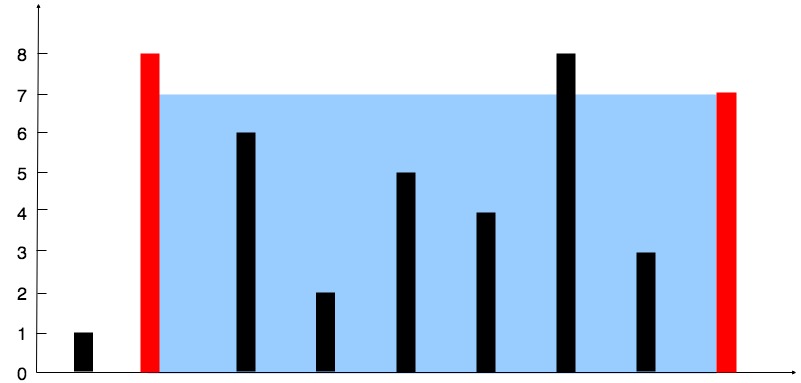
Input: height = [1,8,6,2,5,4,8,3,7]
Output: 49
Explanation: The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.

Example 2:

1
2
Input: height = [1,1]
Output: 1

Example 3:

1
2
Input: height = [4,3,2,1,4]
Output: 16

Solving The Problem

To solve the problem let’s think about the all the possible cases including edge cases,

• Maximum elements at start and end of array => [10,3,2,1,15] => Answer = 40
• Empty array => [] => Answer = 0
• One element array => [7] Answer = 0

Here, it’s very clear that to find the area of water between two heights we need to multiply the minimum of the heights with the width which is equal to the difference between array indices of the same elements.

height = min(heights[i], heights[j])

width = j-i

area = height x width

The Solution

With the above formula in mind let’s move forward to solve this problem programmatically. As usual, we will find all areas between all the possible pairs of elements in the array and take return the maximum. This will be a brute force method and such a coding solution would look like,

We know the problem with this approach is it would take O(n²) time complexity. That’s the reason we need to find an optimal solution that would give us better time complexity.

The Optimal Solution

In this solution, we will traverse the array using a single loop and two pointers from either of the edges. We will move the pointer inwards if it is less than or equal to the other one. We repeat this operation until the two pointers meet and compare all the possible area values to get the maximum area. The following is the code solution for this.

As we can see this will only iterate the array once and no nested loops are present the run time complexity of this method will be O(n)

References

• Container with most water on LeetCode