Count Complete Tree Nodes
According to Wikipedia, every level, except possibly the last, is completely filled in a complete binary tree, and all nodes in the last level are as far left as possible. It can have between 1 and 2h nodes inclusive at the last level h.
The Problem
Given the root of a complete binary tree, return the number of the nodes in the tree.
Design an algorithm that runs in less than O(n) time complexity.
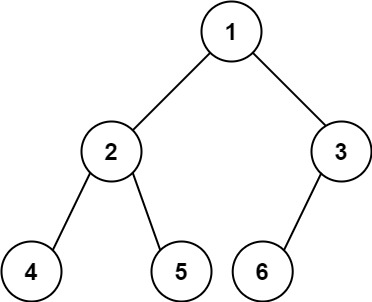
Example 1

1
2
Input: root = [1,2,3,4,5,6]
Output: 6
Example 2
1
2
Input: root = []
Output: 0
Example 3
1
2
Input: root = [1]
Output: 1
The Solution
In the first look, this problem would look simple since it’s just counting the total number of nodes which we can do using BFS or DFS as we have done earlier. But both of those methods would take O(n) run time complexity as it scans through all the nodes in the tree and in the question it’s specifically mentioned the solution should be < O(n). The major complexity classes less than O(n) are O(log n) and O(1). So let’s think about such a solution.
A complete binary tree can have the nodes fully filled in the last level or partially filled in the last level but all nodes in the last level are as far left as possible according to the definition. So if we leave the last level, we can easily calculate the number of nodes in the remaining tree(The upper part) using the formula,
Nodes in upper tree = 2h - 1
This calculation only takes O(1) complexity. The variable h here is the maximum height of the given tree. To find h we can use the following logic which would take O(log n) time complexity
Now the only part remaining is the last level. This level can be treated as a sorted array since it will have non-null values in the left and maybe from some point to the right it can have null values. So we can find the point from which null values started using the Binary Search approach. To do that,
- Find the mid of the last level nodes and check if the node is null
- If the value is null, then the position we are looking for will be on the left side so we can continue the binary search on the left side
- Otherwise, continue BS on the right side.
- Finally, we will get the index after which all the values are null. We can add 1 to this index to get the number of nodes in the last level since the index starts from 0.
The number of nodes at the last level added with the number of nodes in the upper tree gives us the total number of nodes in the tree. Check out the code for the above logic here,
Also, the function to check if the node exists will be,
The run time complexity of the whole logic here to find the number of nodes in a complete binary tree is O(log2 n) which is less than O(n).
References