Cycle Detection in a Linked List

Today we are going to solve a very interesting concept in linked lists that is cycle detection. There is a cycle in a linked list if there is some node in the list that can be reached again by continuously looping through the elements.
The Problem
Given a linked list, return the node where the cycle begins. If there is no cycle, return null.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that the tail’s next pointer is connected to. Note that pos is not passed as a parameter.
Notice that you should not modify the linked list.
Example 1:
1
2
3
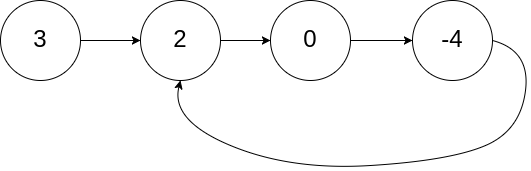
Input: head = [3,2,0,-4], pos = 1
Output: Tail connects to node index 1
Explanation: There is a cycle in the linked list, where the tail connects to the second node.
Example 2:
1
2
3
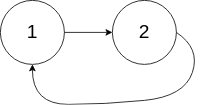
Input: head = [1,2], pos = 0
Output: tail connects to node index 0
Explanation: There is a cycle in the linked list, where the tail connects to the first node.
Example 3:

1
2
3
Input: head = [1], pos = -1
Output: No cycle
Explanation: There is no cycle in the linked list.
The Solution
The first method that comes to our mind is to loop through the linked list and check if the current element is one of the already visited elements. If yes we can return the current element position as the point where the loop starts. This is pretty straight forward and lets try to write the program,
The time complexity of this problem is O(n) but the disadvantage of this method is we have to use extra space for storing the already seen elements which can grow up to O(n). Let’s see if we can solve this problem without using extra space.
The Optimal Solution
To optimise the solution we have already written, we will be using Floyd's Tortoise And Hare Algorithm.
Using this algorithm we initiate two pointers tortoise and hare where the first one will move one place at a time and the second will be moving two places in one iteration.
If there’s a cycle according to Floyd’s algorithm these two pointers will meet at some point.
To find the element from which the cycle started, we can initiate a pointer from the head at the moment when tortoise and hare met and then increment that pointer and the pointer at the met place one step at a time until they both meet.
The new meeting place will be the place from which the cycle started.
Let’s try to write that in code,
The time complexity of this solution will also be O(n) but since we are not taking any extra memory space this method will be more efficient than the previous one.
References